In Visual Basic, write a program to determine the real roots of the quadratic equation after requesting the values of a, b, and c.  Before finding the roots, ensure that a is nonzero.  Note:  The equation has 2,1, or 0 solutions depending on whether the value of b^2 – 4*a*c is positive, zero, or negative.  In the first two cases, the solutions are given by the quadratic formula:

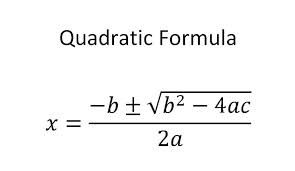
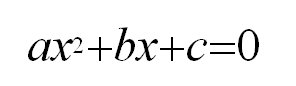
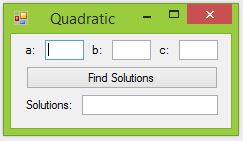
Below is an example of what the application should look like:

Hints:

• There will either be 0, 1 or 2 solutions to the equation
• If the discriminant of the equation (the part of the numerator under the square root) is a negative number, there are no real solutions.
• If the discriminant is zero, there will only be one solution.
• If the discriminant is positive, there will be two solutions.

Suggested Control Names and Attributes:

Name Property	Text Property	Control Type	Notes
frmQuadratic	Quadratic	Form	Holds Controls
txtA		TextBox	Captures value of “A” variable
txtB		TextBox	Captures value of “B” variable
txtC		TextBox	Captures value of “C” variable
btnSolution	Find Solutions	Button	Triggers event to display solutions
txtSolutions		TextBox	Displays solutions

Write the Code:

' Project: Quadratic Equation
' Programmer: Janice Wallace
' Date:  July 26, 2014
' Description:  Solves the quadratic equation

Public Class frmQuadratic

    Private Sub btnSolution_Click(sender As Object, e As EventArgs) Handles btnSolution.Click
        Dim varA As Integer = CInt(txtA.Text)
        Dim varB As Integer = CInt(txtB.Text)
        Dim varC As Integer = CInt(txtC.Text)
        Dim discriminant As Integer = (varB * varB) - (4 * varA * varC)
        Dim solution1 As Double = 0
        Dim solution2 As Double = 0

        ' Check to make sure A is a positive number
        If (varA = 0) Then
            MessageBox.Show("The value of A cannot be zero.")
        End If

        ' If the disciminant is negative there is no real solution
        If (discriminant < 0) Then
            txtSolutions.Text = "There is no solution"
        End If

        ' If the discriminant is zero there is one solution
        If (discriminant = 0) Then
            solution1 = (-varB / 2 * varA)
            txtSolutions.Text = "One solution: " & solution1
        End If

        ' Otherwise there are two solutions
        If (discriminant > 0) Then
            solution1 = ((-varB + Math.Sqrt(discriminant)) / (2 * varA))
            solution2 = ((-varB - Math.Sqrt(discriminant)) / (2 * varA))
            txtSolutions.Text = "Two solutions: " & solution1 & " and " & solution2
        End If

    End Sub
End Class